My Research



The (persistent) homology of periodic cell complexes
Invited talks:
- 30th October 2024, Combinatorics, Geometry and Topology Seminar, Institute of Science and Technology Austria.
- 23rd October 2024, DataShape Seminar, Laboratoire de Mathématiques d'Orsay
- 10th May 2024, Oxford Applied Topology Seminar, Oxford University
- 23rd May 2023, London TDA Seminar, Queen Mary University of London London
- 5th December 2022, EPFL Applied Topology Seminar, EPFL (Slides)
- 23rd August 2022, London TDA Seminar, Queen Mary University of London
Contributed talks:
- 9-13th December 2024, Joint Meeting of the NZMS, AustMS and AMS, University of Auckland
- 23-27th September 2024, ComPerWorkshop 2024, Graz University of Technology
- 9-11th April 2024, British Applied Mathematics Colloquium, University of Newcastle
- 20-24th June 2022, ATMCS10, Oxford University
Preprints:
- Persistent local systems of periodic shapes, A.O. & P. Skraba, 2025
- Computing 1-periodic persistent homology with finite windows, A.O. & P. Skraba, 2023
- Quantifying the homology of periodic cell complexes, A.O. & V. Robins, 2022
A d-periodic cell complex is a cell complex which permits a free action by a free abelian group of rank d. These model very large, homogeneous data sets. Think, for instance, of a graph modelling a crystal - which has translational symmetries. The problem is that any finite representation that we study does not respect its overall topology without additional data. These representations lose some topological features of the infinite periodic complex and also create new topological features. For instance, the maximal quotient graph with respect to translation of disconnected 3-periodic graph in the image has a single connected component and three single edge 1-cycles.
My research uses algebraic techniques to attempt to reconstruct the homology of a periodic cell complex from a finite representative (with minimal additional data). Most recently, I have been working with Dr Amit Patel to achieve this with objects known as "bisheaves".
I am also interested in the question of how to determine when two finite spaces represent the same periodic space, but have made less progress on this front (but see here for some cool work by another group working on this problem).
Generalised persistent homology transforms
Invited talks:
- 11th March 2025, Swansea/Durham TDA Reading Group
- 18th February 2025, Statistics and Data Science Seminar, Queen Mary University of London
Contributed talks:
- 21-25th July 2025, ATMCS11, Montana State University
Preprint:
- Shoving tubes through shapes gives a sufficient and efficient shape statistic, A.O., N. Otter & R. Turkes, 2024
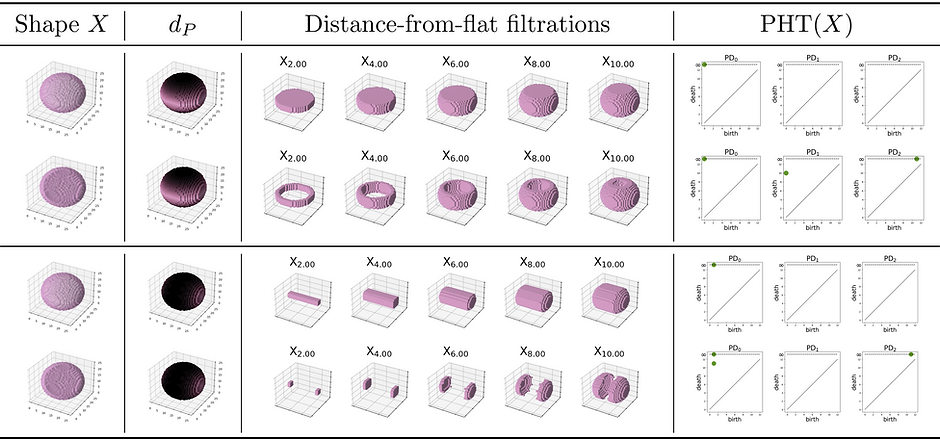
Turkes, Montufar & Otter introduced the notion of a tubular filtration as a means to detect convexity in data. A tubular filtration of a set X by a like l is a filtration on X induced by the sublevel sets of the distance to l. In particular, they were able to show that any triangulisable subset of Euclidean space is convex iff the tubular filtration with respect to every straight line has trivial persistent homology in degree 0.
In fact, this family of filtrations is able to detect much more than convex, as one can show it is a complete statistics on constructible subsets of Euclidean space, much like the Persistent Homology Transform first introduced by Turner, Mukherjee & Boyer. To this end, I am currently working with Dr Nina Otter and Dr Renata Turkes to extend the theory and practical applications of tubular filtrations. So far, we have extended this to an entire family of distant-to-flat persistent homology transforms which are sufficient shape statistics in Euclidean space, and we have future plans to look at implementations, finite approximations and computational bounds, stability results and extensions to non-Euclidean spaces.
Undergraduate projects
My undergraduate degree at ANU allowed me to complete a number of research projects during and in place of coursework
Theoretical Astrophysics: Emission lines from electron excitations in cyanide (HCN) molecules have been shown to have a strong correlation with star formation rates. I was able to do a project with Christoph Federrath and Mark Krumholz analysing numerical simulations to determine an empirical relationship between star formation rates and HCN emission. This was the first calibration of its kind worldwide and lead to a paper which you can view here.
Algebraic Geometry: In a class on computational algebraic geometry taught by Martin Helmer, I was able to do a fun report on how one can use techniques from algebraic geometry to solve graph colouring problems and sudoku puzzles (and vice versa). I created some working Macaulay2 code which uses this to solve sudoku puzzles (and their 2x2 equivalent shidoku) in an admittedly unfeasibly long time.
Theoretical Physics: I was able to do a research project with David Williams which involved analytical and numerical computations of how coplanar and coaxial molecular gears interact via a Lennard-Jones potential.